- 배열(array) : 동일한 데이터 유형의 요소를 순차적으로 저장하는 데이터 구조. 한 번에 여러 개의 변수를 생성 가능.
ex) 10개의 정수를 저장할 수 있는 배열은 다음과 같이 선언. s는 배열의 이름이고 s 안에는 10개의 정수를 저장 가능.
- int s[10];

- 이러한 배열은 인덱스를 사용하여 각 요소에 액세스할 수 있다. 이를테면, 배열의 첫 번째 요소는 인덱스 0에 위치하며, 두 번째 요소는 인덱스 1에 위치하고, 이런식으로 계속된다. 변수 선언이 단독 주택이라면 배열은 아파트 단지이다. 단독 주택에는 한 가구만 살지만, 아파트 단지에는 여러 가구가 동시에 거주할 수 있다. 배열의 이름은 아파트 단지 이름으로 생각할 수 있고 인덱스는 아파트의 호수에 해당한다.
- 인덱스(index) : 배열 안에 들어있는 각각의 데이터들은 번호에 의하여 식별된다. 이 번호를 인덱스라고 한다. 인덱스는 0부터 시작한다.
- 배열 요소(array element) : 배열에 저장된 데이터. 배열의 크기가 10이면 배열 요소는 0에서 9까지이다.
- 배열에서는 인덱스를 이용하여 배열 요소에 접근한다.
- 배열이 필요한 이유 : 정수형 변수 10개를 선언한다고 할 때, int s0, s1,...,s9;과 같은 방법으로 선언하면 오래 걸린다. int s[10]이 훨씬 간단하다.
- 배열의 특징 : 배열은 메모리의 연속적인 공간에 저장된다. 예를 들어서 앞에서의 배열 요소 s[0]과 s[1]은 실제 메모리상에서도 서로 붙어있다. 또한 배열의 가장 큰 장점은 서로 관련된 데이터를 차례로 접근하여 처리할 수 있다는 점이다. 만약 관련된 데이터들이 서로 다른 이름을 사용하고 있다면 이들 이름을 일일이 기억해야 할 것이다. 그러나 하나의 이름을 공유하고 단지 번호만 다를 뿐이라면 아주 쉽게 기억할 수 있고 편리하게 사용할 수 있다. 배열은 근본적으로 데이터들에 하나하나 이름을 붙이지않고 전체 집단에 하나의 이름을 부여한 다음, 각각의 데이터에 숫자로 된 번호를 붙여서 접근하는 방법이다.
- 배열의 선언 : 배열을 사용하려면 먼저 배열을 선언해야 한다. 배열 선언을 통해 컴파일러에게 배열의 요소의 개수가 몇 개이고 각 요소의 자료형이 무엇인지를 알려야 한다. 배열을 선언하려면 먼저 자료형을 지정하여야 한다. 다음으로 배열의 이름이 나오고 대괄호를 붙인 다음에 대괄호 안에 배열의 크기를 적어주면 된다. ex) int s[10]
참고) 배열의 크기를 나타낼 때는 항상 정수 상수를 이용하여야 한다. 변수를 배열의 크기로 사용하면 컴파일 오류가 발생한다. 또한, 배열의 크기를 음수나 0, 실수로 하면 모두 컴파일 오류이다.
참고) 보통 배열을 선언할 때는 배열의 크기를 #define 지시자로 만들어진 기호 상수로 지정한다.
ex)
#define SIZE 10
int s[SIZE];
#define을 이용한 기호 상수로 배열의 크기를 지정하게 되면 배열의 크기를 변경하기가 쉬워진다. 즉, 프로그램의 다른 부분을 수정하지 않고 단지 기호 상수의 정의만 바꾸면 된다.
- 배열 요소 접근 : 배열 요소에 접근하려면 s[5]와 같이 대괄호 안에 요소의 인덱스(번호)를 적어주면 된다.
- 유효한 인덱스의 범위는 0에서 (배열 크기 -1)까지이다.
- 배열 요소는 변수와 100% 동일하므로 값을 배열 요소에 저장 가능. 배열 요소에 저장된 값을 꺼낼 수도 있음.
ex) s[5] = 80;을 하면 5번째 요소에 80이 저장된다.
ex) s[3] = s[2];를 하면 2번째 요소를 3번째 요소로 복사한다.
- 배열을 사용할 때, 인덱스가 배열의 크기를 벗어나게 되면 프로그램에 치명적인 오류를 발생시킨다. 컴파일러는 프로그래머가 유효 범위 안에 있는 인덱스를 사용하고 있는지를 확인하여 주지 않는다. 그러므로 조심하여야 한다.
- 배열의 초기화
- 배열은 여러 개의 변수가 모인 것이므로 초깃값도 하나가 아니고 배열 크기만큼의 값이 필요하다. 배열을 초기화하려면 초깃값들을 콤마로 분리하여 중괄호 {}로 감싼 후에 이것을 배열을 선언할 때 대입해주면 된다. 배열은 선언하면서 동시에 초기화할 수도 있다.
ex) int s[5] = { 10, 20, 30, 40, 50 };
- 위의 문장에서는 5개의 요소로 된 배열 s를 선언한다. 첫 번째 요소 s[0]은 10으로 초기화되며, s[1]의 초깃값은 20이고 이런 식으로 계속된다.
- 만약 초깃값의 개수가 배열 요소의 개수보다 많은 경우에는 컴파일 오류가 된다. 만약 초깃값의 개수가 요소들의 개수보다 적은 경우에는 앞에 있는 요소들만 초기화되며 나머지 배열 요소는 0으로 초기화된다.
- 초기화만 하고 배열의 크기를 비워놓으면 컴파일러가 자동으로 초깃값들의 개수만큼 배열의 크기를 잡는다.
- 만약 초깃값이 주어지지 않았고 함수 안에 선언되었다면, 일반 변수와 마찬가지로 아무 의미 없는 쓰레기값이 들어가게 된다.
참고) int scores[] = {10, 9, 5, 4, 1, 11}; 이라는 배열이 있을 때, 배열 요소의 개수를 계산하려면 size = sizeof(scores) / sizeof(scores[0]); 과 같이 sizeof 연산자를 이용하면 된다.
- 배열의 복사 방법 :
int i;
int a[SIZE] = {1,2,3,4,5};
int b[SIZE];
for(i=0;i<SIZE;i++)
b[i] = a[i];
- 배열의 비교도 a==b(배열의 이름은 배열이 저장된 메모리 주소와 같으므로 배열의 내용이 아니라 각각 배열 주소를 비교하는 것임)가 아니라 위처럼, 배열의 요소끼리 for 문을 이용하여 비교해주어야 한다.
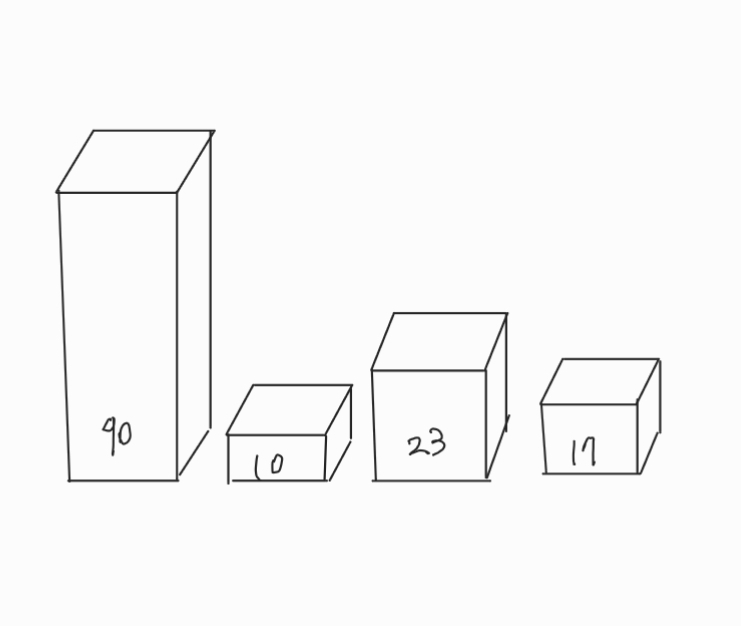
- 버블 정렬
- 정렬(sorting) : 물건을 크기순으로 나열하는 것.
- 정렬에는 많은 방법이 존재한다. 그 중 가장 간단한 버블 정렬은 가장 효율적인 정렬 방법은 아니지만, 가장 이해하기 쉽다.
- 버블 정렬 순서 :
(1) 인접한 블록 2개를 비교하여서 순서대로 되어 있지 않으면 위치를 바꾼다. 이 과정을 리스트의 마지막 블록까지 되풀이한다. 이것을 하나의 패스라고 하자. 첫 번째 패스가 종료되면 가장 큰 값은 제 위치에 있다.
(2) 다시 인접한 블록 2개를 비교하여서 순서대로 되어 있지 않으면 위치를 바꾼다. 두 번째 패스가 끝나면 그 다음으로 큰 값이 제 위치에 온다.
(3) 위의 과정을 블록의 개수만큼 되풀이하면 모든 블록이 크기순으로 정렬된다.
* 인접한 두 변수의 값을 바꿀 때, 임시 변수 tmp를 사용하여야한다.
- 2차원 배열
- 다차원 배열은 배열 요소를 다차원으로 가질 수 있다. 다차원 배열에는 2차원 배열, 3차원 배열 등 일반적으로는 n차원 배열이 가능하다. 그러나 다차원이 되면 필요 메모리 공간이 급격하게 늘어나므로 주의해야한다.
ex) int a[6]; 은 1차원 배열, int b[4][6]; 은 2차원 배열, int c[3][4][6]; 은 3차원 배열이다.

- 2차원 배열 : 배열의 요소들이 2차원으로 배열되어 있다.
- 따라서 행(row)과 열(column)을 나타내는 2개의 인덱스를 가짐.
- 엑셀의 워크시트와 같은 구조를 2차원 배열이라고 생각하면 됨.
- int s[3][5]; 에서 앞의 [3]은 행의 개수, 뒤의 [5]는 열의 개수다.
- 2차원 배열에서 요소 참조
- 2차원 배열에서 하나의 요소를 참조하려면 2개의 인덱스가 필요.
- 위의 배열 int s[3][5]; 는 s[0][0], s[0][1],...,s[2][3], s[2][4]까지 모두 15개의 요소를가진다.
- 2차원 배열 전체를 초기화하려면 변수 i를 0에서 (행의 수 -1)까지 변경시키고 변수 j를 0에서 (열의 수 -1)까지 변경시키면서 s[i][j]에 값을 저장하면 된다.
- 2차원 배열의 초기화 : 2차원 배열도 1차원 배열과 마찬가지로 선언과 동시에 초기화 가능. 다만 같은 행에 속하는 초깃값들을 중괄호 {}로 따로 묶어주어야 한다.
ex)
int s[3][5] = {
{ 0, 1, 2, 3, 4 },
{ 10, 11, 12, 13, 14},
{ 20, 21, 22, 23 24 }
}
'프로그래밍 언어 > C언어_기초 프로그래밍' 카테고리의 다른 글
| [ C언어 기초 ] 8. 함수 (13) | 2024.09.24 |
|---|---|
| [ C언어 기초 ] 6. 반복문 (2) | 2024.09.16 |
| [ C언어 기초 ] 5. 조건문 (7) | 2024.09.16 |
| [ C언어 기초 ] 4. 수식과 연산자 (0) | 2024.09.04 |
| [ C언어 기초 ] 3. 자료형 (1) | 2024.08.28 |